Kara – Programmieren mit endlichen Automaten
Kara für Profis!
Es ist erstaunlich, welche Aufgaben mit endlichen Automaten
gelöst werden können. Eine kleine Auswahl von solchen
Aufgaben finden Sie hier.
Kara besucht jedes Labyrinth vollständig!
Ein Beitrag vonHorst Müller, Institut für Informatik, Universität Erlangen.
|
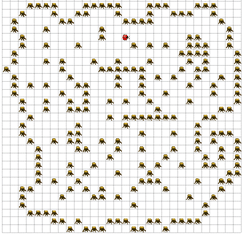 Kann Kara einen beliebigen zusammenhängenden Raum vollständig besuchen und jedes Feld mit einem Kleeblatt belegen? Kara kann sich keine "Landkarte" der Welt aufbauen, um sich so zu merken, wo er schon war oder wo es Bäume hat.
Kann Kara einen beliebigen zusammenhängenden Raum vollständig besuchen und jedes Feld mit einem Kleeblatt belegen? Kara kann sich keine "Landkarte" der Welt aufbauen, um sich so zu merken, wo er schon war oder wo es Bäume hat.
Obwohl Kara nur seine unmittelbare Umgebung wahrnimmt, kann er diese Aufgabe lösen. Horst Müller bewies 1977 in "A One-Symbol Printing Automaton Escaping from every labyrinth", Computing, Band 19, pages 95-110, 1977, dass ein endlicher Automat beliebige Labyrinthe vollständig besuchen kann. Eine verbesserte Version findet sich in Horst Müller, "Improvements on Printing Mice in Labyrinths", Computing, Band 47, pages 235-246, 1992.
Das Unterfangen ist allerdings aufwendig: der von Horst Müller definierte endliche Automat für diese Aufgabe umfasst 7968 Zustände. Kara darf im Vergleich zu "normalen" endlichen Automaten pro Zustandsübergang mehr Befehle ausführen, so dass ein Kara-Automat mit weniger Zuständen auskommen würde. Horst Müller schätzt die benötigte Anzahl Zustände trotzdem noch auf mehrere Hundert...
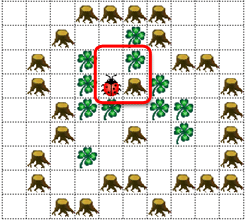 |
Die Kernidee bei den Algorithmen von Horst Müller ist ein für Labyrinth-Probleme klassisches Backtracking-Verfahren. Dazu müssen besuchte Felder geeignet markiert werden, zum Beispiel "von daher ist Kara gekommen". Diese Markierung wird simuliert, indem vier Felder zu einem "Makrofeld" zusammengefasst werden. Man überlegt sich, wie auf den nicht durch Bäume besetzen Teilen eines Makrofeldes durch teilweise Belegung mit Blättern Markierungen angebracht werden können. So kann man mit Kara und der Welt als Speicher Backtracking implementieren! |
Weitere Informationen von Horst Müller:
|
Kara, die Ameise
|
 Aus der Mathematik sind Beispiele von einfachen Iterationen bekannt, die komplexes Verhalten aufweisen.
Das wohl berühmteste Beispiel ist das Apfelmännchen.
Es gibt auch einfache endliche Automaten, die ein sehr komplexes Verhalten aufweisen. Ein Beispiel sind Christopher Langton's Ameisen (Spektrum der Wissenschaften, August 1995).
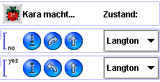
Die Langton-Ameise kann mit Kara einfach simuliert werden. Steht Kara auf einem Feld ohne Kleeblatt, so legt er ein Kleeblatt und geht auf das Feld rechts; steht Kara auf einem Feld mit Kleeblatt, so nimmt er es auf und geht auf das Feld links. Die Abbildung links zeigt das entsprechende Kara-Programm.
Aus der Mathematik sind Beispiele von einfachen Iterationen bekannt, die komplexes Verhalten aufweisen.
Das wohl berühmteste Beispiel ist das Apfelmännchen.
Es gibt auch einfache endliche Automaten, die ein sehr komplexes Verhalten aufweisen. Ein Beispiel sind Christopher Langton's Ameisen (Spektrum der Wissenschaften, August 1995).
Die Langton-Ameise kann mit Kara einfach simuliert werden. Steht Kara auf einem Feld ohne Kleeblatt, so legt er ein Kleeblatt und geht auf das Feld rechts; steht Kara auf einem Feld mit Kleeblatt, so nimmt er es auf und geht auf das Feld links. Die Abbildung links zeigt das entsprechende Kara-Programm.
 |
Das interessante an diesem Programm ist sein Verhalten: sieht es anfangs chaotisch aus, so beginnt die Ameise, Kara, nach rund 10'000 Übergängen eine Struktur zu bauen, die von ihrem Entdecker James Propp "Autobahn" genannt wurde. Die Ameise scheint stets in die Phase des Autobahnbaus zu geraten, sogar dann, wenn zu Beginn beliebig Kleeblätter in der Welt gelegt werden. Langton's Ameise regt zum Experimentieren an: Man kann die Muster betrachten, die bei verschiedenen Anfangskonfigurationen entstehen oder das Programm geringfügig ändern. |
Quellen:
|
Kara, der fleissige Biber
|
|
Was ist mit einer Turing-Maschine berechenbar bzw. entscheidbar und was nicht?
Das Standard-Beispiel eines nicht entscheidbaren Problems ist das Halte-Problem:
eine Turing-Maschine soll entscheiden, ob eine andere Turing-Maschine
je anhält oder nicht.
Von Tibor Rado (1962) stammt ein Beispiel einer einfachen nicht-berechenbaren
Funktion. Für eine gegebene Anzahl n betrachtet man
Turing-Maschinen mit n Zuständen (Stopzustand wird dabei nicht gezählt), die beginnend
auf einem leeren Band irgendwann anhalten. Die Funktion S(n)
soll die maximale Anzahl Markierungen (nicht notwendigerweise zusammenhängend)
bestimmen, die eine Turing-Maschine mit n Zuständen auf
dem Band hinterlassen kann, bevor sie anhält.
Solche Turing-Maschinen werden "fleissige Biber" genannt.
Die Funktion ist zwar wohldefiniert, aber schon für kleine n (ab 5, 6, ...)
ist der Wert von S(n) nicht bekannt.
Der fleissige Biber mit 4 Zuständen hinterlässt 13 Markierungen auf dem Band.
Heiner Marxen zeigte, dass der fleissige Biber mit 5 Zuständen mindestens 4098 Markierungen auf dem Band und
der fleissige Biber mit 6 Zuständen mindestens 1.29*10865 Markierungen hinterlässt.
In Dewdney's "Der Turing Omnibus" wird ein Resultat von
M. W. Green von 1964 zitiert, das eindrücklich zeigt, was
"unberechenbar" bei diesem Beispiel heisst:
Für jede berechenbare Funktion f gilt für alle Werte von n:
f(S(n)) < S(n+1). Das heisst, S(n) wächst
schneller als jede berechenbare Funktion!
 |
Mit Kara lassen sich Turing-Maschinen einfach simulieren, zumindest
solche mit endlichen, nicht allzu grossen Bandlängen. Horst Müller
hat den fleissigen Biber mit 4 Zuständen in Kara umgesetzt.
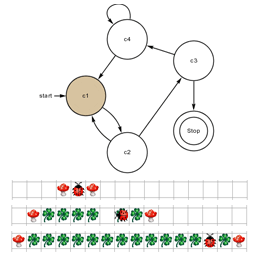
Die Pilze in der Abbildung links werden nur verwendet, um zu zeigen,
welchen Bandbereich Kara bisher betreten hat; die drei Streifen
zeigen die Anfangskonfiguration der Welt (leerer Streifen),
eine Zwischenaufnahme und die 13 Kleeblätter nach Beendigung
des Programms.
Da Kara im Gegensatz zu einer Turing-Maschine pro Zustandsübergang
mehr als einen Befehl ausführen kann, lassen sich die Resultate zu Turing-Maschinen nicht eins-zu-eins auf Kara übertragen. Wieviele Kleeblätter der fleissigste Kara mit 3, 4, 5 Zuständen legen kann, ist offen.
|
Quellen:
- Tibor Rado: On Non-Computable Functions, The Bell System Technical
Journal, vol. XLI, no. 3, May 1962, pp. 877-884.
- Heiner Marxen, Tabelle mit den bisher bekannten Zahlen zu fleissigen Bibern:
Heiner Marxen, Jürgen Buntrock:
Attacking the Busy Beaver 5, Bulletin of the EATCS, Number 40, February 1990, pp. 247-251, [ISSN 0252-9742]
- Horst Müller, Programm für fleissigen Biber mit 4 Zuständen:
fleissigerbiber4.kara.
- A. K. Dewdney: Der Turing Omnibus - Eine Reise durch die Informatik
mit 66 Stationen. Springer, Berlin, 1997, ISBN 3-540-57780-7.
|