K aus Entropie und Energie

Die Gleichgewichtskonstante K einer Reaktion lässt sich aus den Grössen ΔH_R, ΔS_R und ΔG_R folgendermassen berechnen:

(1)\[K = e^{\frac{ - \Delta G_R}{R·T}} = e^{\frac{ - (\Delta H_R - T·\Delta S_R) }{R·T}} = e^{\frac{ - \Delta H_R}{R·T} + \frac{\Delta S_R}{R}}\]

Dieser Zusammenhang ist nicht einfach zu verstehen. Einigen Aspekte kann man jedoch anhand von Gedankenexperimenten ganz gut auf die Spur kommen.

K und ΔS K und ΔE K, ΔS und ΔE

Geschwindigkeit ändern

· 0.5 · 1 · 2 · 5 · 10

Ganzes Dokument expandieren minimieren

K und Reaktions-Entropie ΔS_R

Der Zusammenhang zwischen der Reaktionsentropie und K ist nicht so schwierig zu verstehen. Man kann sich das anhand einer Reaktion überlegen, bei der die Edukte und Produkte gleichen Energieinhalt haben. Die Simulation K und ΔS zeigt diese Situation. Die Entropie ist dann ein Mass für die Anordnungsmöglichkeiten der Edukte und der Produkte. In unserem Modell entspricht dies einfach der Breite des jeweiligen Bodens.

In der Simulation ist der Boden der Produkte doppelt so gross wie der Boden der Edukte. Die Produkte haben also doppelt Anordnungsmöglichkeiten. Die Wahrscheinlichkeit, dass ein Edukt-Teilchen in einem Zeitintervall reagiert, ist daher doppelt so gross wie die Wahrscheinlichkeit, dass ein Produkt-Teilchen reagiert. Und so liegen im Gleichgewicht auch doppelt so viele Produkt-Teilchen vor. Wenn W_Edukte die Anzahl der Anordnungsmöglichkeiten der Edukte beschreibt und W_Produkte die Anzahl der Anordnungsmöglichkeiten der Produkte, so gilt also:

(2)\[K = \frac{W_{Produkt}}{W_{Edukt}}\]

Dieses Resultat ist eigentlich recht simpel. Kompliziert wird es nun nur, weil die Entropie eine logarithmische Grösse ist. Nun entspricht aber die Entropie dem Logarithmus der Anordnungsmöglichkeiten, multipliziert mit der Idealen Gaskonstante:

(3)\[S = R · ln(W)\]

Bzw. umgekehrt:

(4)\[W = e^{\frac{S}{R}}\]

Setzt man dies oben ein, erhält man:

(5)\[K = \frac{W_{Produkt}}{W_{Edukt}} = \frac{e^{\frac{S_{Produkt}}{R}}}{e^{\frac{S_{Edukt}}{R}}} = e^{\frac{S_{Produkt} - S_{Edukt}}{R}}\]

Was schlussendlich ergibt:

(6)\[K = e^{\frac{ΔS_R}{R}}\]

Fazit: Dieser Ausdruck sieht zwar ziemlich kompliziert aus, was aber nur daran liegt, dass die Entropie eine logarithmische Grösse ist. Wäre die Entropie einfach die Anzahl Anordnungsmöglichkeiten, so wäre die Formel recht simpel.

K und Reaktions-Energie ΔE_R

Den Zusammenhang zwischen K und dem Energieunterschied der Niveaus zeigt die Simulation K und ΔE. In einer Welt aus gleichgestuften Niveaus stellt sich eine Verteilung ein mit umso weniger Teilchen auf einem Niveau, je höher das Niveau liegt. Immer für zwei benachbarte Niveaus wird ein Q berechnet und dargestellt. Wenn man die Simulation über längere Zeit betrachtet, sieht man, dass die verschiedenen Q im Durchschnitt denselben Wert einnehmen. Dies macht durchaus Sinn.

Betrachten wir nur die ersten beiden Niveaus. Weil das zweite Niveau etwas höher liegt als das erste, so befinden sich dort im Durchschnitt etwas weniger Teilchen. Der Faktor sei x: auf dem oberen Niveau befinden sich x mal so viele Teilchen wie auf dem unteren.

Betrachten wir nun das zweite und das dritte Niveau. Hier ist der Energieunterschied genau gleich. Überhaupt ist die Situation genau gleich, also wird sich hier dasselbe Teilchenverhältnis einstellen: wieder wird auf dem oberen Niveau etwas weniger Teilchen befinden, und wieder wird der Faktor im Durchschnitt x sein. Auf dem dritten Niveau befinden sich daher x · x = x² mal so viele Teilchen wie auf dem untersten. Auf dem vierten Niveau werden sich daher x³ mal so viele Teilchen befinden wie auf dem untersten, und auf dem fünften Niveau x⁴. Es ergibt sich also auch hier ein exponentieller Zusammenhang: K nimmt mit der Höhe der Niveaus exponentiell ab. Wir können für die Formel eine beliebige Basis wählen - üblicheweise verwendet man die eulersche Zahl e. Die Energie im Exponenten muss mit einem Faktor multipliziert werden, nennen wir ihn \(\beta\). Wie gross dieser Faktor ist, können wir an dieser Stelle noch nicht sagen.

(7)\[K = e^{ \beta {-ΔE_R}}\]

Folgende Abbildung stellt dies nochmals dar.

K, ΔE_R und Temperatur T

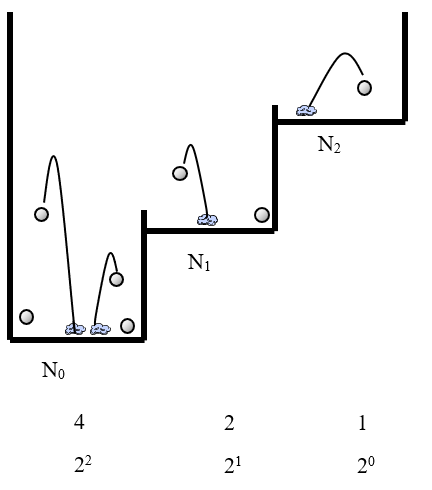
Nehmen wir an, ein System (links) befinde sich im Gleichgewicht. Betrachten wir zwei Teilchen (alle anderen sind ausgeblendet). Das linke Teilchen kommt mit grosser Reserve über die Aktivierungsbarriere (es springt von seinem Niveau aus etwa doppelt so hoch wie seine Aktivierungsenergiebarriere), während es das rechte Teilchen so heb chleb über den Berg schafft.

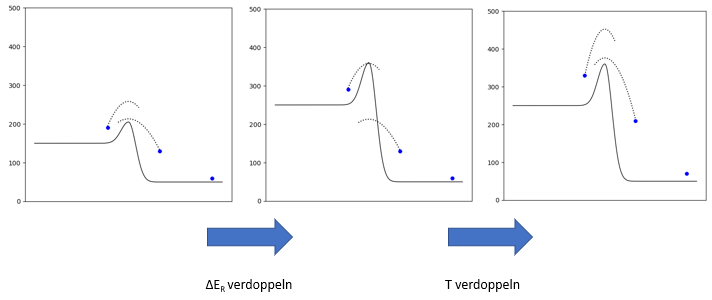
Wenn wir die Höhenunterschiede in der Energielandschaft verdoppeln (Aktivierungsenergien und Reaktionsenergien), so haben wir eine ganz andere Situation. Die Teilchen schaffen es nun nicht mehr über die Aktivierungsenergie-Barriere. Höchstwahrscheinlich verschiebt sich dadurch die Gleichgewichts-Lage.

Wenn man aber zudem die thermische Energie aller Teilchen verdoppelt (also die kinetische Energie plus die potentielle Energie jedes Teilchens über seinem Niveau), dann erinnert die Situation wieder viel mehr an den Ausgangszustand. Das rechte Teilchen überschreitet die Aktivierungsenergie-Barriere wieder ganz knapp, während das linke Teilchen die Barriere mit grosser Reserve schafft (es springt wieder von seinem Niveau aus etwa doppelt so hoch wie die Aktivierungsenergie). Staucht man zudem die y-Achse um den Faktor 2, so sieht die Situation sogar wieder genau gleich aus wie zu Beginn:

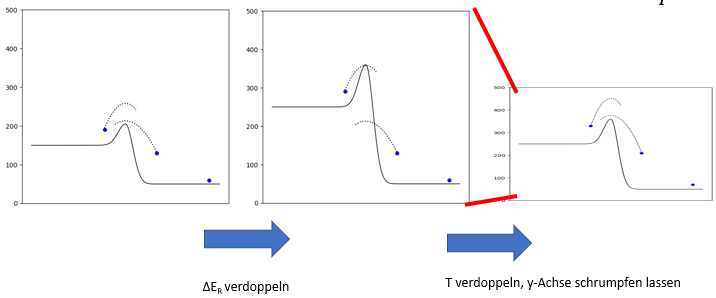
Wir können also sagen: wenn die Reaktionsenergie um den Faktor x erhöht wird, und die Thermische Energie ebenfalls, so herrscht wieder dasselbe Gleichgewicht. Für die Gleichgewichtskonstante K ist also das Verhältnis aus ΔE und thermischer Energie bzw. T entscheidend: entscheidend ist der Quotient \({\frac{- ΔE_R}{T}}\).

Dieser Quotient sagt, wie gross die Energiebarriere ist im Vergleich zu der thermischen Energie, die den Teilchen zur Überwindung der Energiebarriere zur Verfügung steht. Es ist also klar, dass K von einer Exponentialfunktion von \({\frac{- ΔE_R}{T}}\) abhängt: Es braucht natürlich auch da einen Faktor k (über oder unter dem Bruchstrich, wir setzen ihn mal darunter ein):

\(K = e^{\frac{- ΔE_R}{k \cdot T}}\)

Somit erhält man für den obigen Faktor \(\beta\):

\(\beta = \frac{1}{k \cdot T}\)

Tatsächlich ist dieser Faktor k ausgerechnet \({k_B}\) (bzw. \({R}\)). Dieser Zahlwert von k lässt sich nicht so einfach plausibilisieren (jedenfalls habe ich keinen Weg gefunden). Die Gleichgewichtskonstante ergibt sich also aus T und \(- ΔE_R\) zu:

\(K = e^{\frac{- ΔE_R}{k_B \cdot T}}\)

K, ΔS_R, ΔE_R und T

Betrachten wir nun nur wieder ein Modell mit zwei Niveaus, und die Niveaus seien zunächst gleich breit. Wie wir nun wissen, stellt sich ein Gleichgewicht ein mit \(K = e^{\frac{- ΔE_R}{R·T}}\).

Nun wird das obere Niveau auf das x-fache verbreitert. (Simulation K, ΔS und ΔE) Da nun die Anordnungsmöglichkeiten auf dem oberen Niveau x-fach grösser werden, wird K auch um den Faktor x zunehmen:

(8)\[K = e^{\frac{- ΔE_R}{R·T}} · f\]

Wir können nun aber den Faktor f auch als Funktion der Entropie ausdrücken. Wir wissen ja bereits, dass gilt:

(9)\[K = \frac{W_{Produkt}}{W_{Edukt}} = e^{\frac{ΔS_R}{R}}\]

Da in unserem Fall W_Produkt f-mal so gross ist wie W_Produkt erhalten wir:

(10)\[K = e^{\frac{ΔS_R}{R}} = \frac{W_{Edukt} · f }{W_{Edukt}} = f\]

f ist in unserem Fall also nichts anderes als \(e^{\frac{ΔS_R}{R}}\), so dass wir für den kombinierten Effekt von Energie und Entropie erhalten:

(11)\[K = e^{\frac{- ΔE_R}{R·T}} · e^{\frac{ΔS_R}{R}} = e^{\frac{- ΔE_R}{R·T} + \frac{ΔS_R}{R}} = e^{\frac{- (ΔE_R - T·ΔS_R)}{R·T}}\]

K und ΔG_R

Für ganz bestimmte Bedingungen gelten diese Überlegungen für ΔE_R dieses Modells auf für die Reaktionsenthalpie ΔH_R: Man kann die Überlegungen übertragen, wenn eine Reaktion unter konstantem Druck abläuft und sich am Schluss wieder dieselbe Temperatur wie zu Beginn einstellt, wie dies in der Chemie üblich ist.