Wellen
Wellen
Inhalt
- Mehrfachspalt
- Schwingende Saite, Wellen auf einer räumlichen Dimension
- de Broglie-Atom
- Potentialtopf
- Zeigerwellen
- Schraubenwellen
- Schwingende Membran
- Strahlungsübergang
- Farbwellen
Jeweils Abbildung anklicken, um Animation zu starten.
Doppelspalt und Mehrfachspalt
Zweidimensionale Wellen im Doppelspalt
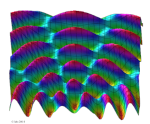
Zusammenrückender Doppelspalt
Zwei Spalten werden immer näher zusammengerückt.
Vom Einfachspalt zum 16fach-Spalt
Neben einem einzelnen Spalt werden mehr und mehr zusätzliche Spalten eingeführt.
- Vom Einfach- zum Doppelspalt
- zum 16fach-Spalt, seitlich
- zum 16fach-Spalt, von oben
- zum 16fach-Spalt, abnehmender Spaltabstand
Einzel- und Doppelspalt
Einzelspalt (für Animation anklicken)
Doppelspalt (für Animation anklicken)
Doppelspaltexperiment erklärt:
Dreidimensionale Welle im Doppelspalt

Um das Verhalten von Wellen im Doppelspalt zu verstehen, studiert man am besten zweidimensionale Wellen im Doppelspalt (nächster Abschnitt), bei denen
man die Interferenz der Wellen nach dem Durchtritt durch den Doppelspalt genau studieren.
Quanten (wie Elektronen) sind allerdings nicht zweidimensional, sie lassen sich hingegen als dreidimensionale Wellen verstehen. Die
Animation eines dreidimensionalen Quants im Doppelspalt
zeigt, wie eine räumliche Welle durch einen Doppelspalt hindurchtritt.
Die Isofläche umfasst jeweils einen bestimmten Anteil der Wahrscheinlichkeitsdichte des Quants (z.B. innerhalb der Fläche ist "90% des Quants zu spüren"). Die Phase des Quants an jeder Stelle ist durch Farben dargestellt. Bei einer Farbe und ihrer Komplementärfarbe ist die Phase jeweils entgegengesetzt. Genaueres unter Farbwellen. Die hintere Wand sei ein Bildschirm, an dem das Quant hängen bleibt (Der das Quant gewissermassen zwingt, sich für eine bestimmte Stelle auf dem Bildschirm zu entscheiden). Nach dem Durchtritt erscheint das Quant also zufällig an irgend einer Stelle auf dem Bildschirm. Dabei taucht es mit erhöhter Wahrscheinlichkeit an einer Stelle auf, bei der die Wellenfunktion hinter dem Doppelspalt besonders gross war (hohe Wahrscheinlichkeitsdichte), also irgendwo im Inneren der Isofläche.
Der eigentliche Messvorgang, bei dem die ausgedehnte Wellenfunktion verschwindet und das Quant in einem Bereich auf dem Bildschirm auftaucht, ist hier nicht dargestellt (siehe Quanten)
Schwingende Saite
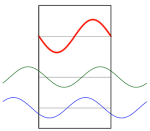
Schwingungen in einer räumlichen Dimension (zum Animieren jeweils Abbildung anklicken)
Laufende und stehende Wellen
Schwingende Saiten (unterschiedliche Frequenz)
Laufende Wellen auf einer Saite
- Laufende und stehende Wellen in einem Kasten
- Reflexion an Wand
- 1 Buckel
- 2 Buckel
- Ecken
Wellenpaketchen
- Wellenpaketchen
- Identische Gruppen- und Phasengeschwindigkeit
- Gruppengeschwindigkeit grösser als Phasengeschwindigkeit
- Gruppengeschwindigkeit kleiner als Phasengeschwindigkeit
De Broglie-Atom
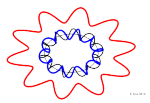
De Broglie-Atom mit laufenden und stehenden Wellen
De Broglie: Atom als schwingende Saite
- De Broglie-Atom 1
- De Broglie-Atom 2
- De Broglie-Atom 3
- De Broglie-Atom 4
- De Broglie-Atom Überlagerung 1 (animiert)
- De Broglie-Atom Überlagerung 2 (animiert)
De Broglie-Atom aus Schraubenwellen
- De Broglie-Atom mit Schraubenwelle Uhrzeigersinn
- De Broglie-Atom mit Schraubenwelle Gegenuhrzeigersinn
- De Broglie-Atom mit stehender Welle aus Schraubenwellen
- De Broglie-Atom aus Schraubenwellen
Potentialtopf

Linearer Potentialtopf
- Linearer unendlich tiefer Potentialtopf, Wellenfunktion
- Linearer unendlich tiefer Potentialtopf, Wahrscheinlichkeitsdichte
- Linearer endlich tiefer Potentialtopf, Wellenfunktion
- Linearer endlich tiefer Potentialtopf, Wahrscheinlichkeitsdichte
Zusammengesetzte Töpfe mit gleicher Energie
Zusammengesetzte Töpfe mit gleicher Energie, gestaucht
Zusammengesetzte Töpfe mit unterschiedlicher Energie
Zusammengesetzte Töpfe mit unterschiedlicher Energie, gestaucht
Harmonischer Potentialtopf
- Harmonischer Potentialtopf, Wellenfunktion
- Harmonischer Potentialtopf, Wahrscheinlichkeitsdichte
Atomähnlicher Potentialtopf
Zusammengesetzte Töpfe, gestaucht
Zeigerwellen
- Zeigerwelle
- Zeigerwelle und Farbwelle
- Schwebung aus Zeigerwellen
- Schwebung aus Zeigerwellen und Farbwellen
Ebene Wellen (Schraubenwellen)
Welle, deren Amplitude überall gleich ist ("Ebene Welle", Schraubenwelle)
Überlagerung gegenläufiger ebener Wellen (Schraubenwellen): Kurven | Überlagerung als Fläche
Wellenlänge 1 (lange)
- Rotierende Welle (Summe von Schraubenwellen) von der Seite
- Rotierende Welle (Summe von Schraubenwellen) von vorn
- Rotierende Welle 3D
Wellenlänge 2
- Rotierende Welle (Summe von Schraubenwellen) von der Seite
- Rotierende Welle (Summe von Schraubenwellen) von vorn
- Rotierende Welle 3D
Wellenlänge 3
- Summe von der Seite
- Summe von vorn
- Schraube a von der Seite
- Schraube a von vorn
- Schraube b von der Seite
- Schraube b von vorn
- Alles von der Seite
- Alles von vorn
Schwingende Membran
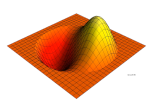
Welchen Orbitalen (1s, 2p, ...) entsprechen folgende Grundschwingungen?
- Schwingung 1
- Schwingung 2
- Schwingung 3
- Schwingung 4
- Schwingung 5
- Schwingung 6
- Schwingung 7
- Schwingung 8
Folgende Schwingungen sind zusammengesetzt aus zwei Grundschwingungen, Aus welchen?
- Überlagerung 1
- Überlagerung 2
- Überlagerung 3
- Überlagerung 4
- Überlagerung 5
- Überlagerung 6
- Überlagerung 7
- Überlagerung 8
- Überlagerung 9
- Überlagerung 10
Folgende Schwingungen entsprechen den angebebenen Orbitalen
Folgende Schwingungen entsprechen den Überlagerungen der angegebenen Orbitale. Was passiert jeweils mit dem schwerpunkt der Auslenkung?
- 1s und 2s, unterschiedliche Frequenz
- 1s und 2px, gleiche Frequenz
- 1s und 2px, unterschiedliche Frequenz
- 2px und 2py, Summe
- 2px und 2py, Differenz
- 2px und 2py, phasenverschoben
- 2px und 2py, phasenverschoben 2
- 2px und 3px, unterschiedliche Frequenzen
- 2px und 3d, gleiche Frequenzy, in Phase
- 2px und 3d, unterschiedliche Frequenz
Strahlungsübergänge
Verschiedene Übergänge lassen sich schön simulieren auf www.falstad.com
Überlagerungen von stehenden Wellen, Strahlungsübergang im linearen Potentialtopf
- Welle n = 1 (Bild anklicken)
- Welle n = 2 (Bild anklicken)
- Welle n = 3 (Bild anklicken)
- Überlagerung von Welle n=1 mit Welle n=2
- Überlagerung von Welle n=2 mit Welle n=3
Strahlungsübergang an Membran
Strahlungsübergang Orbitale
Atomorbitale
Molekülorbitale
- Übergang Wasserstoffmolekül | Übergang Wasserstoffmolekül mit Darstellung der Phase
- Absorption und Konformationsänderung bei Ethen
Farbwellen
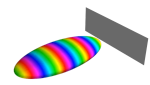
Ein Elektron als Farbwelle
Ein einzelnes Quant, z.B. ein Elektron, weist immer eine bestimmte Ausdehnung im Raum auf. Wie eine Wolke ist es an gewissen Stellen "stärker zu spüren", an anderen nur sehr ausgedünnt.
In der
Animation eines reflektierten Quants als Farbwelle
ist ein solches Quant als rundliches Objekt dargestellt.
Mathematisch beschreibt solche einzelne Quanten mit einer räumlichen Wellenfunktion. An jeder Stelle im Raum weist diese Funktion einen anderen Betrag auf. Dort, wo der Betrag gross ist, ist "viel von dem Elektron zu spüren". Genauer: Aus dem Quadrat dieses Betrages kann man berechnen, wie gross die Wahrscheinlichkeit ist, das Teilchen in einem bestimmten Raumbereich einzufangen. In der Animation sei der Betrag in der Mitte des runden Objekts am grössten und werde nach aussen hin immer kleiner. Die gezeigte Oberfläche umspanne den Teil des Raumes, in dem sich das Elektron mit 90% Wahscheinlichkeit einfangen lässt.
Wellenfunktionen haben aber auch eine Phase, durchläuft also einen innere Periodizität - daher spricht man auch von einer Wellenfunktion und nicht etwa von einer Wolke (nächster Abschnitt: Farbuhr). Bei einer zweidimensionalen Wellenfunktion kann man diese Phase durch eine Auslenkung nach oben oder unten darstellen (vgl. oben,Schwingende Membran). Bei einer dreidimensionalen Welle muss man sie anders darstellen - in der Animation eines reflektierten Quants als Farbwelle werden die Phasen treffender durch Farben dargestellt. Dort, wo das Objekt z.B. rot ist, ist die Phase genau entgegengesetzt zu einer in der Komplementärfarbe gefärbten Stelle (also türkis).
Wenn ein solches Quant reflektiert wird, geschieht etwas interessantes: eine Zeitlang bilden sich stehende Wellen mit Knoten aus. Zu jedem Zeitpunkt treten nur noch zwei Farben auf: eine Farbe und ihre Komplementärfarbe. Genau solche stehenden Wellen bilden sich auch aus, wenn man ein Elektron in einem Atom einsperrt. Man nennt diese stehenden Wellen Atomorbitale. Während das Elektron in unserer Animation entwischt und die stehende Welle wieder verschwindet, können die Elektronen eines Atoms nicht entweichen, und so bleiben die stehenden Wellen dort stabil - und verändern sich nur bei Absorption oder Emission von Energie.
Dreidimensionale stehende Wellen als Farbwellen
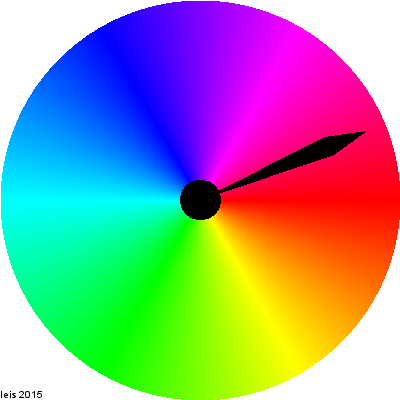
- Hintergrund schwarz | weiss
- Farb-Uhr | Animation
- Zeitwelle | Animation | Animation 2
- Zeitwelle 2 | Animation | Animation 2

Orbitale Isoflächen
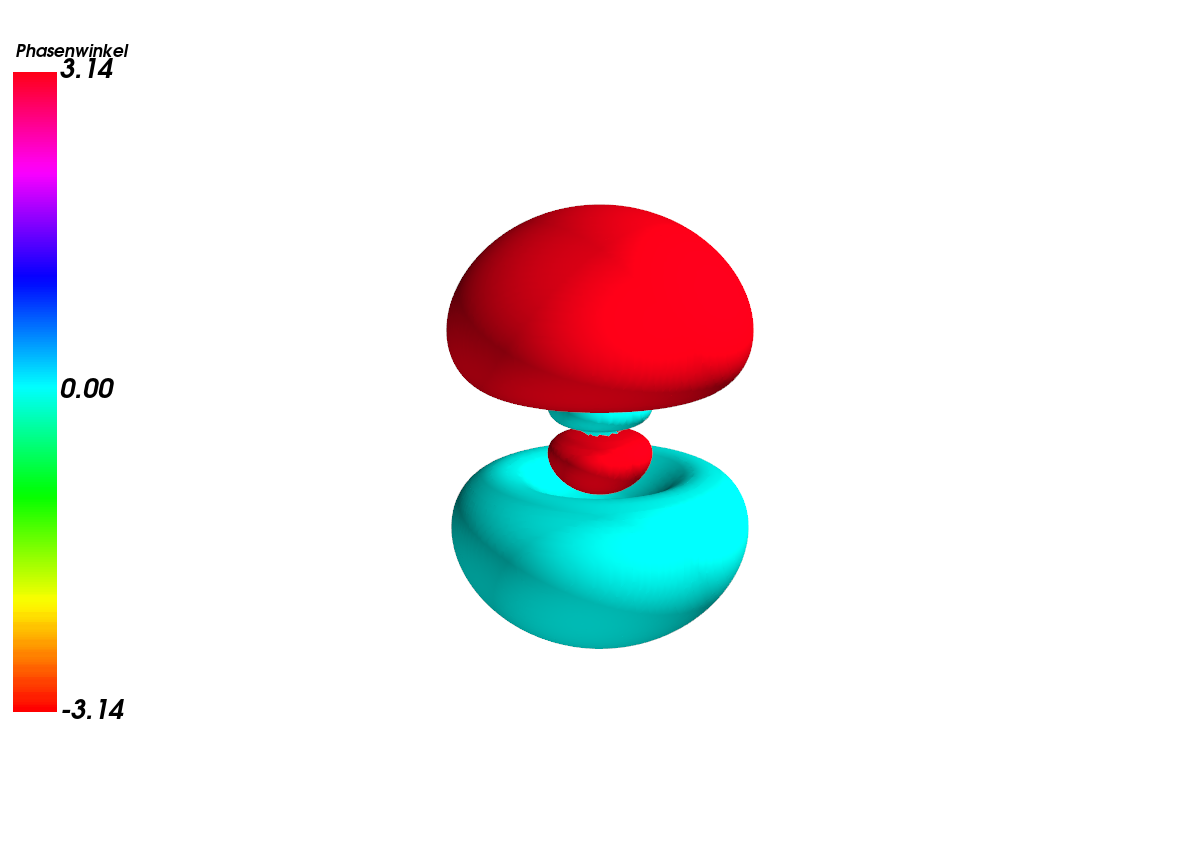

Verschiedene s-Orbitale
- 1p, 2s, 3s - und 4s-Orbitale
- 1s | 2s | 3s | 4s
2p-Orbitale
- Alle komplexwertigen 2p-Orbitale (mit Magnetquantenzahl -1, 0 und +2)
- Alle gerichteten 2p-Orbitale (keine Magnetquantenzahl)
- Zwei komplexwertige 2p-Orbitale (2d+1 und 2d-1) werden übereinandergeschoben, dabei addiert und bilden durch Interferenz 2px
- Zwei komplexwertige 2p-Orbitale (2d+1 und 2d-1) werden anders kombiniert (Subtraktion) und bilden 2py
- 2p0 | 2p+1 | 2p-1 | 2px | 2py
- Alle 3p-Orbitale (komplexwertig)
- Zwei komplexwertige 3p-Orbitale von oben (3p+1 und 3p-1)
- 3p0 | 3p+1 | 3p-1 | 3px | 3py
3p-Orbitale
3d-Orbitale
- Alle komplexwertigen 3d-Orbitale
- 3d+1 und 3d-1 werden zu 3dyz kombiniert
- 3d+2 und 3d-2 werden zu 3dxy kombiniert
- 3d+2 und 3d-2 werden zu 3dx2-y2 kombiniert
- 3d0 | 3d+1 | 3d-1 | 3d+2 | 3d-2 | 3dxz | 3dyz | 3dxy | 3dx2-y2
4f-Orbitale
Orbitale Wolken
(unterschiedliche Frequenzen)
(unterschiedliche Frequenzen)

 Interferenz am Mehrfachspalt
Interferenz am Mehrfachspalt