Kimball- oder Kugelwolkenmodell
Atome
- Wasserstoff-Atom: Elektron und Proton
- Helium-Atom: Zwei Elektronen und Kern
- Lithium-Atom: Drei Elektronen und Kern
- Hypothetisches Lithium-Atom, bei dem beliebig viele Elektronen in einer Kugelwolke Platz finden
- Beryllium-Atom: Valenzelektronen und Rumpf
- Bor-Atom: Valenzelektronen und Rumpf
- Kohlenstoff-Atom mit Kern und Rumpfelektronen oder mit dem Rumpf als einheitliche Kugel
- Stickstoff-Atom. Gäbe es nur elektrostatische Kräfte, würde nicht eine Kugelwolke doppelt besetzt, sondern Kugelwolken würden sich nur teilweise durchdringen.
Moleküle
- Begegnung zweier H-Atome. Solange die Atom symmetrisch sind und sich nicht durchdringen, treten keine resultierenden Krafte auf. Erst eine Asymmetrie führt zur Ausbildung der Bindung.
- Begegnung zweier F-Atome
- Zwei Rümpfe je mit Ladung 7+ und 7 doppelt geladene Kugelwolken ordenen sich an
Drehbarkeit
Grenzen des Kugelwolkenmodells
Ladungsdichteverteilung
Mit Hilfe des Kugelwolkenmodells kann man zwar viel erklären, aber es weist dennoch viele Mängel auf.
Ladungsdichte
Aufgrund des Kugelwolkenmodelles könnte man annehmen, dass es in den Atomen zwischen den Kugelwolken Ränder und Löcher gibt, wo keine Elektronen vorliegen:

Dies ist nicht korrekt: In den Atomen ist die Ladung recht gleichmässig verteilt und es treten weder scharfe Ränder noch Löcher zwischen den Elektronenpaaren auf.
In einzelnen Atomen und Ionen mit Edelgaskonfiguration wie Neon oder Chlorid-Ionen ist die Ladungsverteilung sogar völlig kugelsymmetrisch. Folgende Abbildung zeigt die Elektronendichteverteilung in einem Chlorid-Ion (Cl-) und einem Fluorwasserstoffmolekül (HF):

In jedem Punkt in der dargestellten Fläche ist die Ladungsdichte der Elektronen genau gleich gross. Eine solche Fläche mit konstanter Ladungsdichte heisst Isofläche (der Ladungsdichte).
Folgende Videos zeigen Isoflächen zunehmender Ladungsdichte. Dabei wird die gleichmässige Verteilung der Elektronen gut erkennbar. Am Schluss ist jeweils die Elektronendichte im Rumpf zu sehen.
Zudem sieht man, dass Wasserstoffkerne die Elektronenhüllen leicht verformen (auch dieser Aspekt fehlt im Kugelwolkenmodell).
- Isoflächen zunehmender Elektronendichte Chlorid-Ion
- Isoflächen zunehmender Elektronendichte Methan
- Isoflächen zunehmender Elektronendichte Wasser
- Isoflächen zunehmender Elektronendichte Fluorwasserstoff
Das Kugelwolkenmodell beschreibt die Situation also nur dann befriedigend, wenn man annimmt, dass die Kugelwolken gegen den Rand hin ausdünnen und die ausgedünnten Bereiche überlappen
Mehrfachbindungen: vom Kugelwolkenmodell zu einem Ladungswolkenmodell
Das Kugelwolkenmodell von Ethen lässt vermuten, dass die Bereiche höchster Ladungsdichte in der Doppelbindung oberhalb und unterhalb
der Verbindungslinie zwischen den Kohlenstoffrümpfen liegen (Wasserstoffkerne sind hier nicht eingezeichnet):
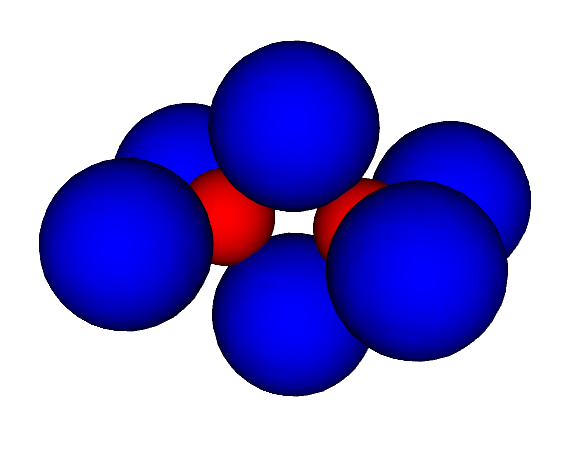
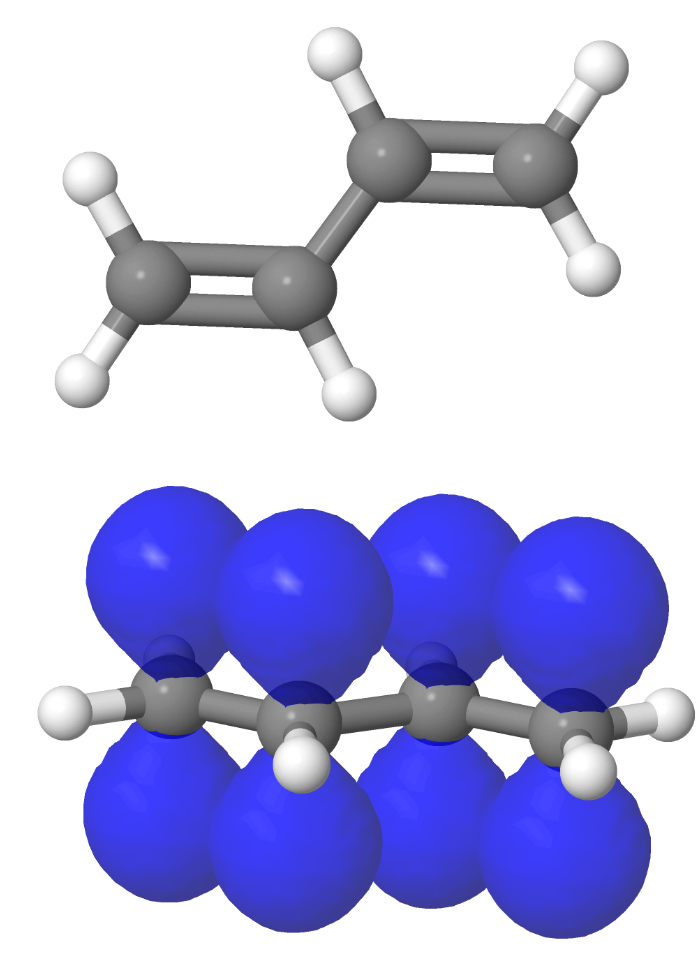
Wieder zeigt aber die Verteilung der Ladungsdichte in Ethen etwas ganz anderes: Die Ladungsdichte der Valenzelektronen ist genau zwischen den Rümpfen am grössten:
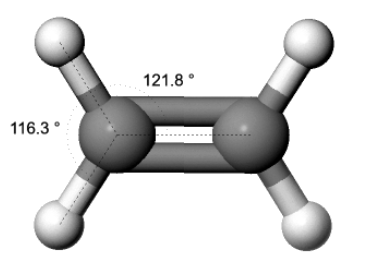
Zudem würde man aufgrund des Kugelwolkenmodells Bindungswinkel von 109.5° zwischen C- und H-Atomen erwarten. Die Winkel liegen aber näher bei 120°:
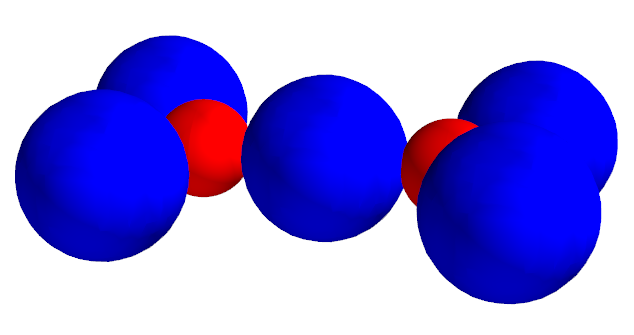
Es ist nicht erstaunlich, dass die höchste Ladungsdichte der Valenzelektronen genau zwischen den Rümpfen liegt, dann dort werden sie ja besonders stark angezogen - nämlich von beiden Rümpfen. Man kann sich also vorstellen, dass eines der Elektronenpaare so stark zwischen die Rümpfe gezogen wird, dass das andere Elektronenpaar ausweichen muss:
Aber wie ordnet sich das andere Elektronenpaar an? In der obigen Animation teilt es sich auf die beiden C-Atome auf. Das ist sicher nicht realistisch. Die ungepaarten Elektronen würden nämlich die anderen Elektronen abstossen und das Molekül dadurch verformen.
Dies kann nicht sein, da die Anordnung der übrigen Elektronen sehr gut mit den Bindungswinkeln übereinstimmt:
Zudem wäre der obere Halbraum über den C-Atomen viel dichter mit Ladung besetzt als der untere.
Im Ladungswolkenmodell (wie im Orbitalmodell) können Elektronenpaare nicht nur "Kugelwolken" besetzen. Sie können auch anders geformte Raumbereiche (Ladungswolken) einnehmen. Der Raumbereich eines Elektrons kann sogar Knoten aufeisen, also Bereiche, wo seine Dichte Null ist. Auch viele Atomorbitale weisen solche Knoten auf. Dies ermöglicht dem zweiten Elektronenpaar eine Anordnung, die mit der Geometrie und der Ladungsdichteverteilung des Moleküls im Einklang ist:
Das zweite Doppelbindungs-Elektronenpaar nimmt also den gesamten Raumbereich ein, der noch nicht dicht mit Elektronen besetzt ist.
Es bildet zwei längliche Lappen oberhalb und unterhalb der C-Atome aus. In der Ebene der Atomkerne hingegen weist das zweite Elektronenpaar einen Knoten auf. Dabei ist wichtig: Beide Elektronen des Elektronenpaares halten sich in beiden Lappen auf. Auch wenn die Ladungswolke nur durch ein Elektron besetzt wäre, so wären doch beide Lappen besetzt.
Die beiden Lappen des zweiten Doppelbindungs-Elektronenpaars ziehen die C-Atome ebenfalls leicht aufeinander zu, sie stellen also auch eine Bindung dar. Diese Bindung aus zwei Lappen ober- und unterhalb der Bindungsachse heisst π-Bindung. Das Elektronenpaar genau zwischen den C-Atomen hingegen stellt eine σ-Bindung dar - wie auch alle C-H-Bindungen. σ-Bindungen sind also kugelsymmetrisch um die Bindungsachse.
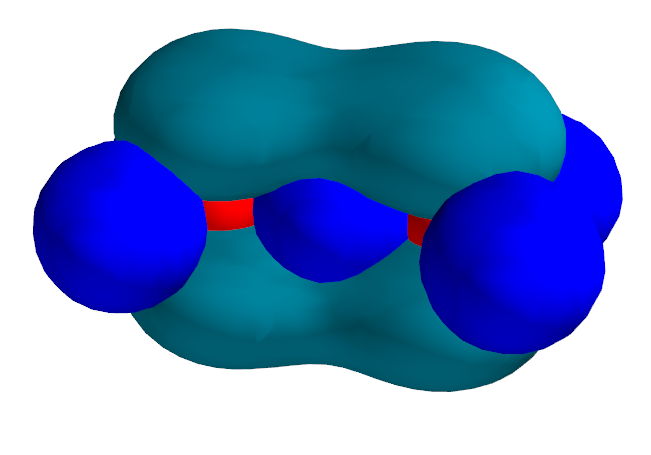
Beispiele für π-Bindungen
Beispiele für π-Bindungen finden sich unter https://www.swisseduc.ch/chemie/molekularium/piSysteme/pi_systeme.htm.